
SplashLearn is available across all digital platforms, and more than 40 million students have used it worldwide. SplashLearn allows students to study math through a highly engaging and customized program. It provides personalized learning for every student according to the 21st century. Splashlearn’s vision is to transform education for K-5th grade students.
EXAMPLE OF SUPPLEMENTARY ANGLE HOW TO
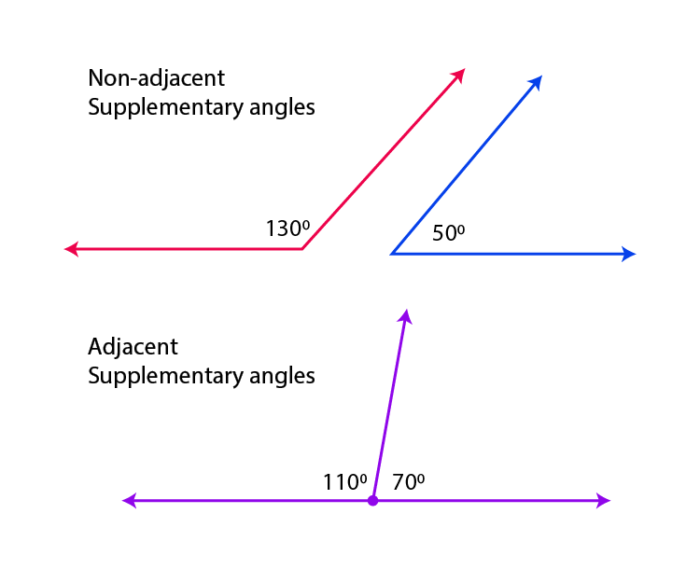
How to Construct an Angle (using protractor) Wall clocks use the concept of angles to show time with hour and minute hands.Artists use their measurement knowledge to sketch or create art pieces.Carpenters use it to make equipment like doors, chairs, sofas, tables, etc.Athletes use its concept in sports to enhance their performance.Engineers construct buildings, bridges, houses, monuments, etc., using angle measurement.Here, ∠AXD and ∠CXD are supplementary angles. Supplementary angles: Angles that add up to 180° (a straight angle) are called supplementary angles. You can use the image above as an example. When two supplementary angles are added together, the result is always 180°. Here, ∠BXC and ∠CXD are complementary angles. Adjacent Supplementary Angles : Adjacent supplementary angles are defined as two supplementary angles that share a common vertex and common arm. Complementary and Supplementary Angles:Ĭomplementary angles: Angles that add up to 90° (a right angle) are called complementary angles. For example, two angles, 130o and 50o are supplementary because their sum, 130o + 50o 180o. Here, ∠ABC, ∠BCA and ∠CAB are interior angles.Įxterior angles: Exterior angles are the angles formed outside a shape, between any side of a shape and an extended adjacent side. Two angles are said to be supplementary if their sum is 180o.

Interior angles: Interior Angles are the angles formed within or inside a shape. A reflex angle measures between 180°- 360°.An angle measuring exactly 180° is a straight angle.For example, if 130 is one angle in Supplementary Angles, then the other angle will be 50. If x is one angle then (180 x) is the other angle in Supplementary Angles. Two angles are added and formed a straight line in Supplementary Angles. A right angle precisely measures 90° at the vertex. The two angles are said to be Supplementary angles if their sum is 180.An obtuse angle is between 90° and 180°.An acute angle measures less than 90° at the vertex.In the given diagram below, OA is the terminal side.īased on their measurements, here are the different types of angles: Terminal Side: The side up to which the angle measurement is done.Initial Side: Also known as the reference line, a straight line from where an angle is drawn.Arms: The two sides of the angle, joined at a common endpoint.Vertex: A vertex is a corner of an angle, a point where two lines/sides meet.Angles are measured in degrees (°) using a protractor.įor example, 45 degrees is represented as 45° Parts of Angles There are many daily life examples of an angle, such as cloth-hangers, arrowheads, scissors, partly opened doors, pyramids, edge of a table, edge of a ruler, etc.

The word angle comes from a Latin word named ‘angulus,’ meaning “corner.” The common point of contact is called the vertex of an angle.

You just have to remember that their sum is 180° and that any set of angles lying along a straight line will also be supplementary.An angle is formed when two straight lines or rays meet at a common endpoint. There isn’t much to working with supplementary angles. The two angles lie along a straight line, so they are supplementary. In the next figure, 3 and 4 are supplementary, because their measures add to 180 °. But, two angles need not be adjacent to be supplementary. The two angles of a linear pair, like 1 and 2 in the figure below, are always supplementary. In the figure, the angles lie along line \(m\). Supplementary angles are two angles whose measures add up to. Let’s look at a few examples of how you would work with the concept of supplementary angles. Since straight angles have measures of 180°, the angles are supplementary.Įxample problems with supplementary angles The angles with measures \(a\)° and \(b\)° lie along a straight line. In the image below, you see one of the common ways in which supplementary angles come up.


 0 kommentar(er)
0 kommentar(er)
